​谢尔宾斯基地毯的维数为()(谢尔宾斯基地毯几何画板)

谢尔宾斯基地毯的维数为()(谢尔宾斯基地毯几何画板)

谢尔宾斯基地毯的维数为()这样可以减少地毯的损耗。但是在实际生产中，由于各种原因，会导致地毯的平均寿命缩短，甚至出现断裂的现象。因此，我们需要根据不同情况采取相应的措施，才能延长地毯的使用寿命。下面我们就来具体了解一下吧。首先，我们需要知道什么是断裂？断裂是指地毯在铺设过程程中出现不规则的裂纹，导致地毯变形、开裂的现象。

用Scratch编程画分形几何图形系列之2：谢尔宾斯基地毯

谢尔宾斯基地毯，是和谢尔宾斯基三角类似的经典分形模型，1917年由波兰数学家谢尔宾斯基发明。它是以正方形为基础单位，依次逐层逐渐拓展成一个无限大的“地毯”状结构。

其递归生成规则是:将一个正方形拆分为9个边长为原来正方形边长三分之一的正方形，去掉正方形中心的小正方形，第二轮对剩下的8个正方形重复这个操作，直至无限生成。如下图所示，生成了两轮。

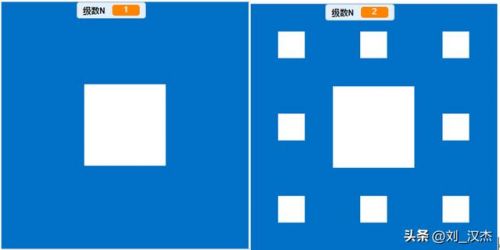
第一轮、第二轮的谢尔宾斯基地毯

我们借鉴谢氏三角的思路，用递归的算法来实现这个生成机制，把去掉中间的小正方形，变成在空白的大正方形的四周依次生成8个长度为原来三分之一的小正方形就OK了。

首先我们先定义一个画实心正方形的模块（子程序），便于在递归的初始状态（级数N=0）时调用。

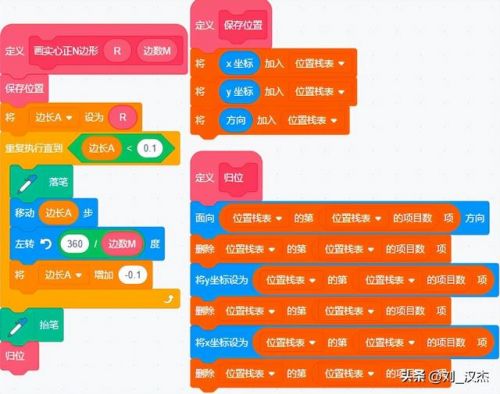
画正方形和位置保存归位的子程序

再来设计递归程序，最初（级数N=0），就是一个画一个正方形，后面每一级都是在上一级正方形的左下开始，依次生成8个长度为上一级三分之一的正方形。在递归算法中仍然使用了保存位置和归位两个子积木（子程序），这个子程序需要建立一个位置列表，保存位置时，依次把当前位置的横坐标x，纵坐标y和方向存入位置列表，回归位置时，则是依次从位置列表里面最后一个元素开始，反向取出来使用，取完一个，立即删掉最后一个元素，这样就能保证下一个取出的是最后一个元素。这就是“堆栈存取规则”，保证回到的是最初的位置。

画谢尔宾斯基地毯的递归子程序

主程序设置好一些初始值，比如图形颜色、递归的层级、分形的尺寸和初始位置和方向。

主程序和第四轮谢氏地毯

谢尔宾斯基地毯具有许多分形的特征，如自相似、无规律的丰富细节等。它在计算机图形学中经常被用作纹理或者形状生成的基础。同时，谢尔宾斯基地毯也是 *** 论中的一个例子，具有一些有趣的性质，如无穷迭代时，生成的 *** 变成了一个分数（非整数）维度的分形，且在空间中的测度为零，但是在带权的测度下却是有限的。关于分形的豪斯多夫维数和测度等概念，以后专门介绍。